In our previous note: Binary Addition with Full Adders we explored how a computational machine performs binary addition. But what about binary subtraction - its mathematical counterpart? Can this be computed using the principles of addition and the hardware of full adders too?

Well, the answer is yes, belive it or not! But to find out how we need to unpick a strange mathematical trick called 'Two's Complement'.

In computing hardware we use the same principles of binary addition to compute subtraction, using a system called ‘two’s complement’. In mathematical terms, this can be expressed as:

A - B = A + (-B) = A + not(B) + 1

The important part of this expression is the bit at the end: A + not(B) + 1. This is two’s complement (the strange mathematical trick) and it states that negative integers can be represented by taking its positive binary value, inverting all the bits and adding 1.

For example, the binary value five (0101) can be represented as -5 in two’s complement notation by following the steps shown in figure 1.

To explain the implication of this a little further, lets tabulate two’s complement notation for all negative integers (-1 to -8) that can be represented by a 4-bit binary value:

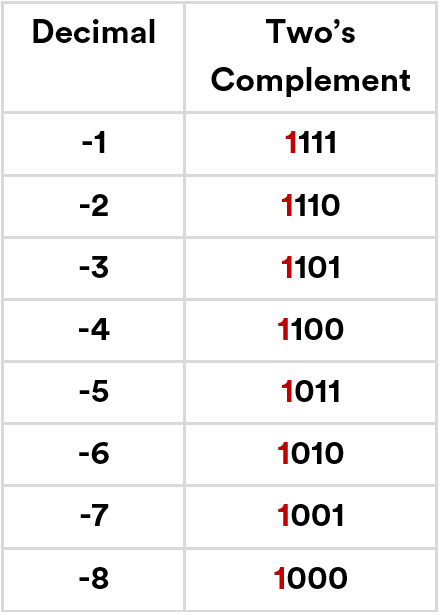
As you can see from the figure 2, negative values represented in two’s complement notation all have something in common – their most significant bit (in red) is 1. This can be thought of as the equivalent of a minus (-) sign.

Using this rule, however, means we cannot represent negative integers beyond -8 using two’s complement on 4-bit values. For example, if we try to convert +9 into -9 using two’s complement we end up with 0111, and this violates our rule that negative numbers begin with 1. Instead, any 4-bit binary value beginning with 0 is treated as a normal positive integer (or zero in the case of 0000). This means the maximum positive integer that can be represented in 4-bit two’s complement is 0111, or 7.

Now we know how to represent 4-bit negative numbers using two’s complement let's perform a simple subtraction of 5 - 5 using the method of binary addition explained in our previous note on addition. If it helps, you can think of this a little more intuitively as the A + (-B) part of the mathematical expression we saw at the beginning of the note.

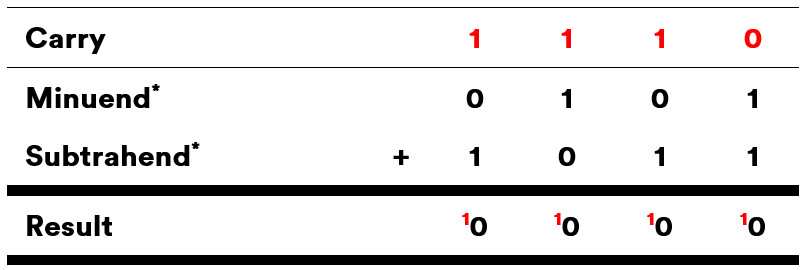
And, indeed, we can see that 5 - 5 does equal zero! The maths checks out!

*A minuend is a number that is subtracted from, and the subtrahend is a number that is subtracted.

So why do we use this slightly weird system? It may seem a little complex, but using this system means the same digital circuitry for addition can be used for subtraction (with some minor modifications) and this makes hardware design much simpler.

For example, subtraction can be implemented on a 4-bit full adder using a quad 2-input XOR IC to invert value B, coupled with an assertion on the full adder’s ‘carry in’ (Cin) to produce the +1, as illustrated below:

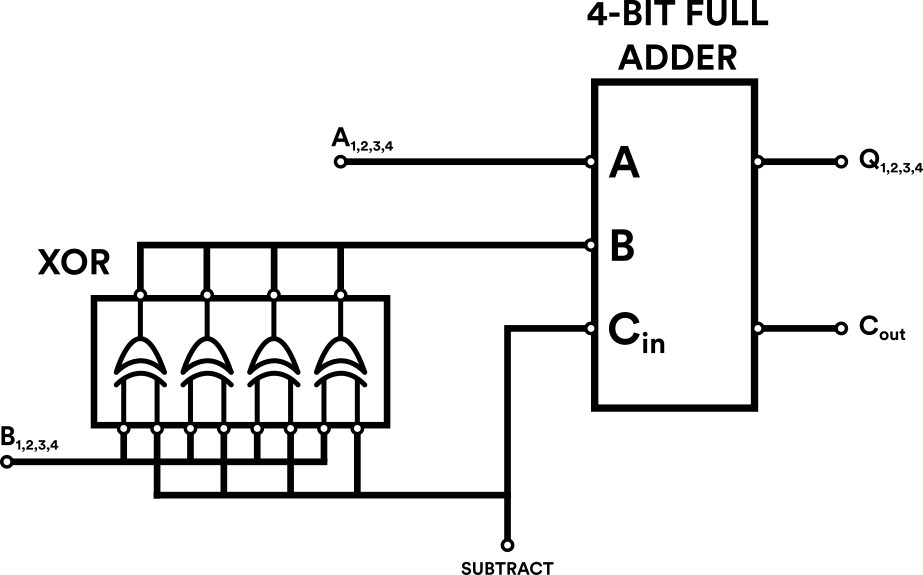
And remember that slightly abstract mathematical expression that describes two’s complement notation: A - B = A + (-B) = A + not(B) + 1? Well, figure 4 is that mathematical expression in action as a digital circuit!

To learn more about computational hardware, why not checkout our next note: Arithmetic Logic Units (ALU): An Introduction.